BP神经网络

一晃又是几个月没更新了，最近面临发paper的问题，想紧跟潮流用深度学习做一些东西，想学习深度学习，先要从神经网络说起。

神经元

　　神经元（Neuron）是构成神经网络的基本单元。人工神经元和感知器非常类似，也是模拟生物神经元特性，接受一组输入信号并产出输出。生物神经元有一个阀值，当神经元所获得的输入信号的积累效果超过阀值时，它就处于兴奋状态；否则，应该处于抑制状态。

　　人工神经元使用一个非线性的激活函数，输出一个活性值。假定神经元接受n个输入$x=(x_1,x_2,\ldots,x_n)$,用状态z表示一个神经元所获得的输入信号x的加权和，输出为该神经元的活性值a。具体定于如下:

\begin{equation}\label{equation1}z = \omega^T x + b\end{equation}

\begin{equation}\label{equation2}a = f(z)\end{equation}

　　其中，w是n维的权重向量，b 是偏置。典型的激活函数f 有sigmoid型函数、非线性斜面函数等。 　　如果我们设激活函数f为0或1的阶跃函数，人工神经元就是感知器。

sigmoid 函数

　　sigmoid 型函数是指一类S 型曲线函数，常用的sigmoid 型函数有logistic 函数$\sigma(x)$ 和tanh(x) 函数。

\begin{equation}\label{equation３}\sigma(x) = \frac{1}{1 + e ^ {-x}}\end{equation}

\begin{equation}\label{equation４}\tanh(x) = \frac{e ^ {x} - e ^ {-x}}{e ^ {x} + e ^ {-x}}\end{equation}

　　logistic函数$\sigma(x)$对应的函数曲线如下图所示：

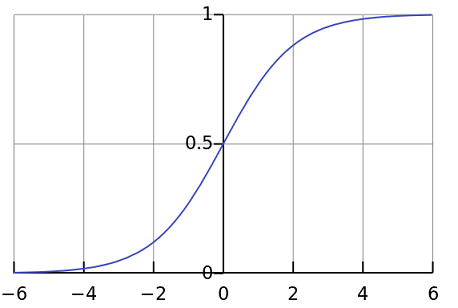
　　tanh函数以看作是放大并平移的logistic函数$tanh(x) = 2\sigma(2x)-1$

　　sigmoid 型函数对中间区域的信号有增益，对两侧区的信号有抑制。这样的特点也和生物神经元类似，对一些输入有兴奋作用，另一些输入（两侧区）有抑制作用。和感知器的阶跃激活函数(−1/1, 0/1) 相比，sigmoid 型函数更符合生物神经元的特性，同时也有更好的数学性质。

　　每一个神经元的模型如下所示

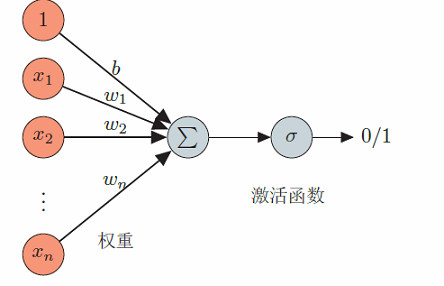
前馈神经网络

　　给定一组神经元，我们可以以神经元为节点来构建一个网络。不同的神经网络模型有着不同网络连接的拓扑结构。一种比较直接的拓扑结构是前馈网络。前馈神经网络（Feed-forward Neural Network）是最早发明的简单人工神经网络。 　　各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第一层叫输入层，最后一层叫输出层，其它中间层叫做隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。 　　一个前馈神经网络如下图所示：

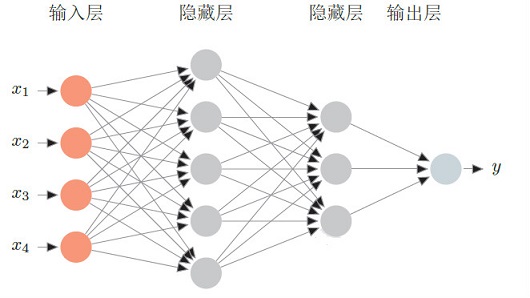
给定一个前馈神经网络，我们用下面的记号来描述这个网络。

L : 神经网络的层数 $n^l$ : 第$l$层神经元的个数 $f_l(\cdot)$ : 第$l$层神经元的激活函数 $\omega^l \epsilon \mathbb{R} ^{n^l*n^{l-1}}$ : 表示$l-1$层到$l$层的权重矩阵 $b^l\epsilon \mathbb{R} ^{n^l}$ : 表示$l-1$层到$l$层的偏置 $z^l\epsilon \mathbb{R} ^{n^l}$ : 表示$l$层神经元的状态 $a^l\epsilon \mathbb{R} ^{n^l}$ : 表示$l$层神经元的活性值

前馈神经网络通过下面公式进行信息传播：

\begin{equation}\label{equation5}z^l =\omega^l \cdot a^{l-1} + b^l\end{equation}

\begin{equation}\label{equation6}a^l = f_l(z^l)\end{equation}

这样，前馈神经网络可以通过逐层的信息传递，得到网络最后的输出$a^L$

反向传播算法

　　既然在输出层产生输出了，那总得看下输出结果对不对吧或者距离预期的结果有多大出入吧？现在就来分析一下什么东西在影响输出。显然，输入的数据是已知的，变量只有那些连接权重了。

　　假定给定一组样本 $(x^i,y^i),1\le i\le N$,用前馈神经网络的输出为$f(x\mid\omega,b)$,目标函数为

\begin{equation}\label{equation7}J(\omega,b)=\sum_{i=１}^NL(y^i,f(x^i\mid\omega,b)) + \frac12 \lambda ||W|| _F^2　\end{equation}

　　这里，$\omega$和b包含了每一层的权重矩阵和偏置向量，$\|W\| _F^2 = \sum_{l=1}^L\sum_{i=1}^{n^l}\sum_{j=1}^{n^{l-1}}\omega_{ij}^l$，$\lambda$表示这个正则项的权重，$\frac12$是便于计算。

　　其中$\omega_{ij}^l$表示$n^{l-1}$层第$j$个节点到第$n^l$层第$i$个节点的权重。 　　我们的目标是最小化这个结构风险函数$J(\omega,b)$，采用随机梯度下降法，用如下方法更新参数，

\begin{equation}\label{equation8}\omega_{ij}^l = \omega_{ij}^l - \alpha\cdot\frac{\partial J(\omega,b)}{\partial \omega_{ij}^l}\end{equation}

　　将公式$(\ref{equation7})$带入上式右边,并对$\|W\| _F^2$进行简化得到：

\begin{equation}\label{equation9}\omega_{ij}^l = \omega_{ij}^l - \alpha\cdot\sum_{m=１}^N(\frac{\partial L(y^m,f(x^m\mid\omega,b)) }{\partial \omega_{ij}^l}) - \alpha\cdot\lambda\cdot\omega_{ij}^l\end{equation}

　　这里$\alpha$是参数的更新率。

　　同样可以得到

\begin{equation}\label{equation10}b_{i}^l = b_{i}^l - \alpha\cdot\sum_{m=１}^N(\frac{\partial L(y^m,f(x^m\mid\omega,b)) }{\partial b_{i}^l})\end{equation}

　　看下$\frac{\partial L}{\partial \omega_{ij}^l}$怎么计算。

　　根据链式法则$\frac{\partial L}{\partial \omega_{ij}^l}$可以改写为

\begin{equation}\label{equation11}\frac{\partial L}{\partial \omega_{ij}^l} =\frac{\partial L}{\partial {z_i}^l}\cdot\frac{\partial {z_i}^l}{\partial \omega_{ij}^l} \end{equation}

　　对于第$l$层，定义一个误差项${\delta_i}^l = \frac{\partial L}{\partial {z_i}^l}$,为目标函数关于第$l$层第$i$个神经元状态的偏导数，来表示第$l$层第$i$个神经元状态对最终误差的影响。公式$(\ref{equation11})$的第一项暂记为${\delta_i}^l$。

　　而${z_i}^l = \sum_{j=1}^{n^{l-1}}\omega_{ij}^l\cdot{a_j}^{l-1}+{b_i}^l$,因此公式$(\ref{equation11})$的第二项就是${a_j}^{l-1}$。

　　公式$(\ref{equation11})$可以改写为

\begin{equation}\label{equation12}\frac{\partial L}{\partial \omega_{ij}^l} = {\delta_i}^l\cdot{a_j}^{l-1} \end{equation}

　　下面到了最关键的时候了，重点分析这个误差项${\delta_i}^l$,根据链式法则，

\begin{equation}\label{equation13}{\delta_i}^l =\frac{\partial {a_i}^l}{\partial {z_i}^l}\cdot\frac{\partial z^{l+1}}{\partial {a_i}^l}\cdot\frac{\partial L}{\partial z^{l+1}} \end{equation}

\begin{equation}\label{equation14}{\delta_i}^l =\frac{\partial {a_i}^l}{\partial {z_i}^l}\cdot(\sum_{s=１}^{n^{l+1}}\omega_{si} \cdot {\delta_s}^{l+1} ) \end{equation}

　　而第$l+1$层每个神经云的状态都与$l$层第$i$个神经元的活性值${a_i}^l$有关。 　　从公式$(\ref{equation14})$可以看出第$l$层的误差项可以通过第$l+1$层的误差项计算得到，这就是误差的反向传播(Backpropagation，BP)。反向传播算法的含义是：第$l$层的一个神经元的误差项（或敏感性）是所有与该神经元相连的第$l+1$层的神经元的误差项的权重和。然后，再乘上该神经元激活函数的梯度。

　　BP神经网络的实现：这是我实现的一个BP神经网络，放在github上。